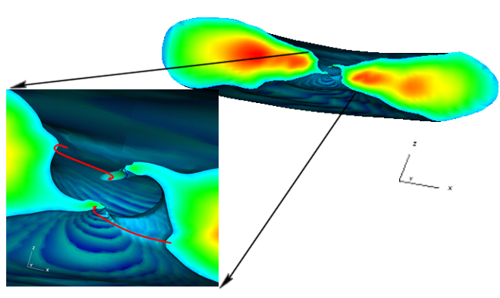
This work represents a continuation of my previous effort to numerically study accretion disks that are misaligned (tilted) with respect to the rotation axis of a Kerr black hole. Recently I completed the first global numerical simulation which fully incorporates the effects of the black hole spacetime as well as magnetorotational turbulence that is the primary source of angular momentum transport in the flow. This simulation shows dramatic differences from comparable simulations of untilted disks. Accretion onto the hole occurs predominantly through two opposing plunging streams that start from high latitudes with respect to both the black-hole and disk midplanes (see figure at right). This is due to the aspherical nature of the gravitational spacetime around the rotating black hole. These plunging streams start from a larger radius than would be expected for an untilted disk. In this regard the tilted black hole effectively acts like an untilted black hole of lesser spin. Throughout the duration of the simulation, the main body of the disk remains tilted with respect to the symmetry plane of the black hole; thus there is no indication of a Bardeen-Petterson effect in the disk at large. The torque of the black hole instead principally causes a global precession of the main disk body. In this simulation the precession has a frequency of 0.3 Hz (for a 10 solar mass black hole), a value consistent with many observed low-frequency quasi-periodic oscillations (QPOs). However, this value is strongly dependent on the size of the disk, so this frequency may be expected to vary over a large range.

Logarithmic density plot of a tilted disk accreting onto a rotating black hole. The figure is oriented such that the black-hole spin axis points straight up. The z-axis of the triad gives the original orientation of the disk angular momentum vector. The main body of the disk shows very little warping or realignment toward the symmetry plane of the black hole. The plunging region (shown in inset) shows two opposing, high-latitude streams of material connecting the disk to the horizon (indicated by arrows).

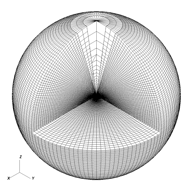
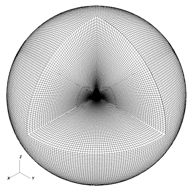
(left) Spherical-polar grid, including underresolved pole region (Fragile et al. 2007b). (right) Cubed-sphere grid composed of six separate subgrids.

In previous work, limitations in computational resources have forced us to under-resolve the pole regions in our three-dimensional tilted-disk simulations when using spherical-polar coordinates (see figure at left). Although underresolving the pole has the desired effect of significantly increasing the Courant-limited timestep (thus reducing the total cycle count), it has the unfortunate consequence of reducing the amount of information we have about what is happening in the region in which jets form. Furthermore, the very nature of spherical-polar coordinates prevents an accurate treatment of fluid transport across the pole. Therefore, we think a new approach is needed for studying jets.

A Cartesian grid would eliminate the anomalous pole features associated with spherical-polar grids. Furthermore the zone geometry would be consistent across the grid so that the global Courant constraint would better match all zones. However, a Cartesian grid has its own drawbacks: 1) it does not naturally concentrate zones near a central object, such as the black-hole event horizon; 2) it does not naturally conserve angular momentum and so introduces additional artificial dissipation into the flow; and 3) it is prone to introducing spurious structure into spherically or cylindrically symmetric flows (such as an m = 4 mode in disks).

Given the limitations of spherical-polar and Cartesian grids, we have recently extended the capabilities of the Cosmos++ code (Anninos et al. 2005) to include a new grid option - the so-called cubed-sphere grid (Koldoba et al. 2002), which stitches together six subgrids in a way that nearly preserves spherical symmetry, yet behaves more like a Cartesian grid, eliminating poles (see figure at left). The cubed-sphere grid option could be further modified to extend selectively along the jet axis without increasing the zone count or spacing around the disk. This is desirable if one wishes to follow the jet out to large distances relative to the size of the disk. Implementing such an unorthodox grid structure is relatively easy within the flexible mesh architecture of the Cosmos++ astrophysics code.